Numerics Namespace Reference

Functions
template<class Shortcuts, typename T>
void	getNormals (const T *Q, int direction, T &norm, T *n)
template<class Shortcuts>
void	getStiffnessTensor (const double *Q, double &c11, double &c22, double &c33, double &c44, double &c55, double &c66, double &c12, double &c13, double &c23)
template<class Shortcuts>
void	computeParameters (const double *Q, double &rho, double &cp, double cs[], int direction)
void	riemannSolverBoundary (int faceIndex, double r, double vn, double vm, double vl, double Tn, double Tm, double Tl, double zp, double zs[2], double &vn_hat, double &vm_hat, double &vl_hat, double &Tn_hat, double &Tm_hat, double &Tl_hat)
template<class Shortcuts, int order, int numberOfVariables, int numberOfParameters>
void	riemannSolver (double *FL, double *FR, const double *const QL, const double *const QR, const double dt, const int direction, bool isBoundaryFace, int faceIndex)
template<class Shortcuts, typename T>
void	computeParameters (const T *Q, T &rho, T &cp, T &cs, T &mu, T &lam)
template<typename T>
void	riemannSolverBoundary (int faceIndex, T r, T vn, T vm, T vl, T Tn, T Tm, T Tl, T zp, T zs, T &vn_hat, T &vm_hat, T &vl_hat, T &Tn_hat, T &Tm_hat, T &Tl_hat)
template<class Shortcuts, typename T, int basisSize, int numberOfVariables, int numberOfData, int surface = 2>
void	riemannSolver (T *FL, T *FR, const T *const QL, const T *const QR, const double dt, const int direction, bool isBoundaryFace, int faceIndex)
template<class Shortcuts, typename T>
void	computeTractions (const T *Q, const T *n, T &Tx, T &Ty, T &Tz)
template<class Shortcuts, typename T>
void	getVelocities (const T *Q, T &vx, T &vy, T &vz)
template<typename T>
void	GramSchmidt (T *y, T *z)
template<typename T>
void	createLocalBasis (T *n, T *m, T *l)
template<typename T>
void	riemannSolverNodal (T v_p, T v_m, T sigma_p, T sigma_m, T z_p, T z_m, T &v_hat_p, T &v_hat_m, T &sigma_hat_p, T &sigma_hat_m)
template<typename T>
void	riemannSolverBC0 (T v, T sigma, T z, T r, T &v_hat, T &sigma_hat)
template<typename T>
void	riemannSolverBCn (T v, T sigma, T z, T r, T &v_hat, T &sigma_hat)
template<typename T>
void	rotateIntoOrthogonalBasis (T *n, T *m, T *l, T Tx, T Ty, T Tz, T &Tn, T &Tm, T &Tl)
template<typename T>
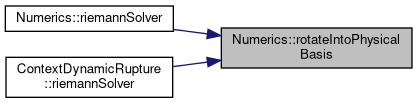
void	rotateIntoPhysicalBasis (T *n, T *m, T *l, T Fn, T Fm, T Fl, T &Fx, T &Fy, T &Fz)
template<typename T>
void	computeFluctuationsLeft (T z, T myT, T T_hat, T v, T v_hat, T &F)
template<typename T>
void	computeFluctuationsRight (T z, T myT, T T_hat, T v, T v_hat, T &F)

Function Documentation

computeFluctuationsLeft()

template<typename T>

void Numerics::computeFluctuationsLeft	(	T	z,
		T	myT,
		T	T_hat,
		T	v,
		T	v_hat,
		T &	F )

Definition at line 172 of file riemannsolverRoutines.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

computeFluctuationsRight()

template<typename T>

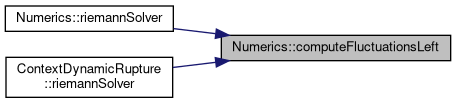
void Numerics::computeFluctuationsRight	(	T	z,
		T	myT,
		T	T_hat,
		T	v,
		T	v_hat,
		T &	F )

Definition at line 177 of file riemannsolverRoutines.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

computeParameters() [1/2]

template<class Shortcuts>

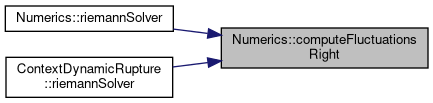
void Numerics::computeParameters	(	const double *	Q,
		double &	rho,
		double &	cp,
		double	cs[],
		int	direction )

Definition at line 25 of file riemannsolverAnisotropic.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

computeParameters() [2/2]

template<class Shortcuts, typename T>

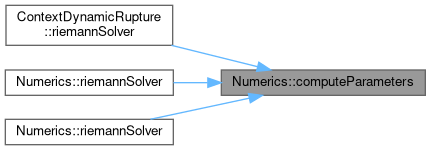
void Numerics::computeParameters	(	const T *	Q,
		T &	rho,
		T &	cp,
		T &	cs,
		T &	mu,
		T &	lam )

Definition at line 10 of file riemannsolverIsotropic.h.

computeTractions()

template<class Shortcuts, typename T>

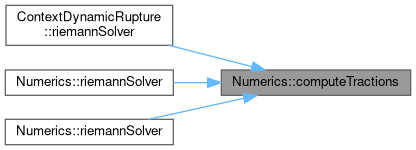
void Numerics::computeTractions	(	const T *	Q,
		const T *	n,
		T &	Tx,
		T &	Ty,
		T &	Tz )

Definition at line 6 of file riemannsolverRoutines.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

createLocalBasis()

template<typename T>

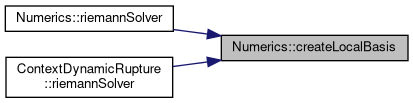
void Numerics::createLocalBasis	(	T *	n,
		T *	m,
		T *	l )

Definition at line 44 of file riemannsolverRoutines.h.

References GramSchmidt().

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the call graph for this function:

Here is the caller graph for this function:

getNormals()

template<class Shortcuts, typename T>

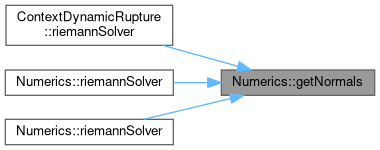
void Numerics::getNormals	(	const T *	Q,
		int	direction,
		T &	norm,
		T *	n )

Definition at line 5 of file cartesianRoutines.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

getStiffnessTensor()

template<class Shortcuts>

void Numerics::getStiffnessTensor	(	const double *	Q,
		double &	c11,
		double &	c22,
		double &	c33,
		double &	c44,
		double &	c55,
		double &	c66,
		double &	c12,
		double &	c13,
		double &	c23 )

Definition at line 11 of file riemannsolverAnisotropic.h.

Referenced by riemannSolver().

Here is the caller graph for this function:

getVelocities()

template<class Shortcuts, typename T>

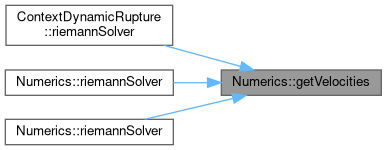
void Numerics::getVelocities	(	const T *	Q,
		T &	vx,
		T &	vy,
		T &	vz )

Definition at line 20 of file riemannsolverRoutines.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

GramSchmidt()

template<typename T>

void Numerics::GramSchmidt	(	T *	y,
		T *	z )

Definition at line 29 of file riemannsolverRoutines.h.

Referenced by createLocalBasis().

Here is the caller graph for this function:

riemannSolver() [1/2]

template<class Shortcuts, int order, int numberOfVariables, int numberOfParameters>

void Numerics::riemannSolver	(	double *	FL,
		double *	FR,
		const double *const	QL,
		const double *const	QR,
		const double	dt,
		const int	direction,
		bool	isBoundaryFace,
		int	faceIndex )

Definition at line 83 of file riemannsolverAnisotropic.h.

References computeFluctuationsLeft(), computeFluctuationsRight(), computeParameters(), computeTractions(), createLocalBasis(), getNormals(), getStiffnessTensor(), getVelocities(), riemannSolverBoundary(), riemannSolverNodal(), rotateIntoOrthogonalBasis(), and rotateIntoPhysicalBasis().

Here is the call graph for this function:

riemannSolver() [2/2]

template<class Shortcuts, typename T, int basisSize, int numberOfVariables, int numberOfData, int surface = 2>

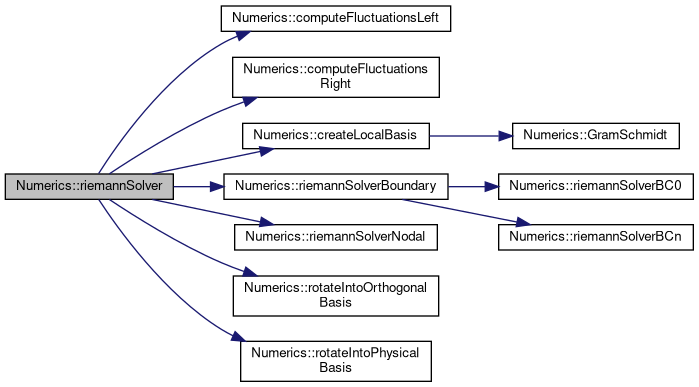
void Numerics::riemannSolver	(	T *	FL,
		T *	FR,
		const T *const	QL,
		const T *const	QR,
		const double	dt,
		const int	direction,
		bool	isBoundaryFace,
		int	faceIndex )

Definition at line 53 of file riemannsolverIsotropic.h.

References computeFluctuationsLeft(), computeFluctuationsRight(), computeParameters(), computeTractions(), createLocalBasis(), getNormals(), getVelocities(), riemannSolverBoundary(), riemannSolverNodal(), rotateIntoOrthogonalBasis(), and rotateIntoPhysicalBasis().

Here is the call graph for this function:

riemannSolverBC0()

template<typename T>

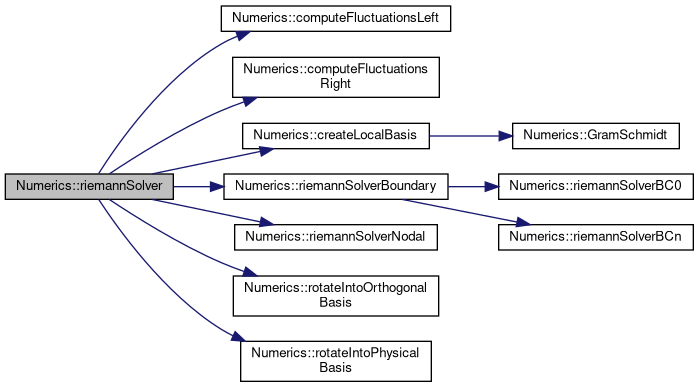
void Numerics::riemannSolverBC0	(	T	v,
		T	sigma,
		T	z,
		T	r,
		T &	v_hat,
		T &	sigma_hat )

Definition at line 129 of file riemannsolverRoutines.h.

Referenced by riemannSolverBoundary(), and riemannSolverBoundary().

Here is the caller graph for this function:

riemannSolverBCn()

template<typename T>

void Numerics::riemannSolverBCn	(	T	v,
		T	sigma,
		T	z,
		T	r,
		T &	v_hat,
		T &	sigma_hat )

Definition at line 141 of file riemannsolverRoutines.h.

Referenced by riemannSolverBoundary(), and riemannSolverBoundary().

Here is the caller graph for this function:

riemannSolverBoundary() [1/2]

void Numerics::riemannSolverBoundary	(	int	faceIndex,
		double	r,
		double	vn,
		double	vm,
		double	vl,
		double	Tn,
		double	Tm,
		double	Tl,
		double	zp,
		double	zs[2],
		double &	vn_hat,
		double &	vm_hat,
		double &	vl_hat,
		double &	Tn_hat,
		double &	Tm_hat,
		double &	Tl_hat )

Definition at line 49 of file riemannsolverAnisotropic.h.

References riemannSolverBC0(), and riemannSolverBCn().

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the call graph for this function:

Here is the caller graph for this function:

riemannSolverBoundary() [2/2]

template<typename T>

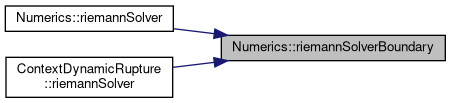
void Numerics::riemannSolverBoundary	(	int	faceIndex,
		T	r,
		T	vn,
		T	vm,
		T	vl,
		T	Tn,
		T	Tm,
		T	Tl,
		T	zp,
		T	zs,
		T &	vn_hat,
		T &	vm_hat,
		T &	vl_hat,
		T &	Tn_hat,
		T &	Tm_hat,
		T &	Tl_hat )

Definition at line 19 of file riemannsolverIsotropic.h.

References riemannSolverBC0(), and riemannSolverBCn().

Here is the call graph for this function:

riemannSolverNodal()

template<typename T>

void Numerics::riemannSolverNodal	(	T	v_p,
		T	v_m,
		T	sigma_p,
		T	sigma_m,
		T	z_p,
		T	z_m,
		T &	v_hat_p,
		T &	v_hat_m,
		T &	sigma_hat_p,
		T &	sigma_hat_m )

Definition at line 81 of file riemannsolverRoutines.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

rotateIntoOrthogonalBasis()

template<typename T>

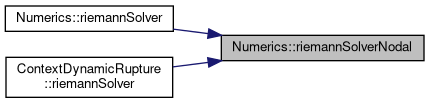
void Numerics::rotateIntoOrthogonalBasis	(	T *	n,
		T *	m,
		T *	l,
		T	Tx,
		T	Ty,
		T	Tz,
		T &	Tn,
		T &	Tm,
		T &	Tl )

Definition at line 153 of file riemannsolverRoutines.h.

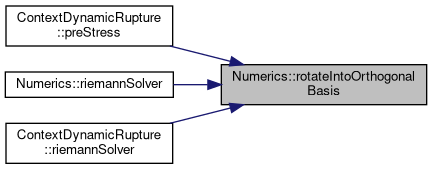
Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::preStress(), ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function:

rotateIntoPhysicalBasis()

template<typename T>

void Numerics::rotateIntoPhysicalBasis	(	T *	n,
		T *	m,
		T *	l,
		T	Fn,
		T	Fm,
		T	Fl,
		T &	Fx,
		T &	Fy,
		T &	Fz )

Definition at line 162 of file riemannsolverRoutines.h.

Referenced by ContextDynamicRupture< Shortcuts, basisSize, numberOfVariables, numberOfParameters, T >::riemannSolver(), riemannSolver(), and riemannSolver().

Here is the caller graph for this function: