Peano's AMR philosophy is guided by few simple principles:

The user recommends mesh properties, and Peano will produce a mesh that is at least as fine as requested. However, the code might decide to work with a finer mesh than requested for various reasons: To create full trees, to avoid topology changes between MPI, and so forth.
Peano adds or removes at most one mesh level at a time.
Peano does not use separate remeshing grid sweeps, i.e. the dynamic adaptivity is integrated into the normal mesh traversals that you also can use to implement your solver's functionality.

AMR workflow and semantics

All AMR instructions in Peano are formalised via objects of the type peano4::grid::GridControlEvent. Each event spans a certain geometric area and is either a refine or an erase event. I try to speak of refine and erase and not of refine and coarsen, as the latter is a term used in a multigrid context and usually means that you still keep the fine data somewhere. In contrast, Peano's erase means that the grid is really thrown away.

Realisation

Prior to each mesh traversal, the automaton running through the mesh asks the active observer hosting one or multiple action sets for a list of grid control events. While is runs through the mesh, it takes these events into account. This happens in three steps:

Each subpartition asks the action set (clone) for the refinement and coarsening decisions at the startup of the mesh traversal. For this, they query getGridControlEvents(). Before we use the events, they are merged/consolidated by peano4::grid::merge().
The mesh traversal uses this information to trigger erases or refinements.
In the subsequent mesh traversal, the mesh is actually altered.

Instruction semantics

The semantics behind the different grid control flags is natural:

refine spans a certain area and hosts a mesh size h. The area spanned should be refined once unless it already hosts a mesh where the spacetree's octant size is already smaller than h.
erase spans a certain area and hosts a mesh size h. The area spanned should be erased unless it would yield a mesh which is coarser than h.

As we work with "at least" semantics all the way through, any refine event overwrites any erase event.

Realisation in the code

or-based refinement and refinement arguments

In Peano, a cell is refined, if one of its vertices carries a refinement flag. That is, we flag vertices (not cells), and the cells are refined if the or combination over all vertices yields true.

Consequently, we adhere to the following AMR paradigms:

All vertices of a cell are set to refine if
1. the cell overlaps with a refine instruction; and
2. the cells' size h is bigger than the refine instruction's mesh size.
All vertices of a cell are set to coarsen if
1. the cell plus all vertex-connected neighbours are completely covered by a erase event; and
2. the cell's size h is smaller than the erase instruction's mesh size.

This behaviour is realised within peano4::grid::Spacetree::evaluateGridControlEvents().

Implication

We study two examples of refinement instructions. In the first example, we start from a regular grid (top) and one refinement instruction specifying that a certain area - in this case not aligned with the grid et al should have a smaller mesh size.

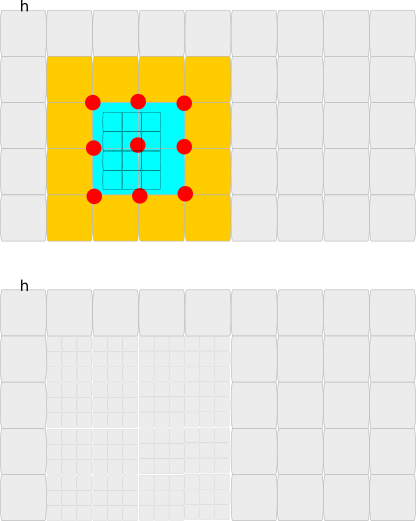
Four cells overlap with the refinement instruction. They set their vertices to refinement-triggered, i.e. nine vertices in total are set to refine. As we have an or-based refinement criterion, this means that all the blueish cells are refined plus the orange ones around them. We end up with the mesh at the bottom.

In the second example, we have an adaptive mesh where an erase condition is imposed with a target mesh size which is just slightly coarser than the h of the right part of the grid.

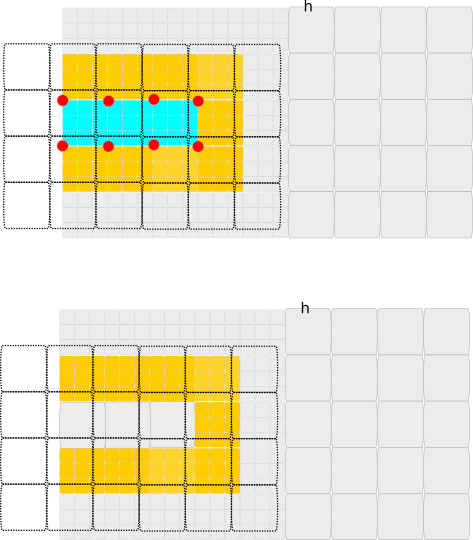
Only refined cells which are overlapped by the erase command together with all of their neighbours are erase candidates. They are marked in blueish, with their adjacent neighbours marked as yellow. Note that Peano thinks in terms of trees and mesh hierarchies. The sketch shows the arising fine grid, but the decision to erase is made on the next coarser mesh within the tree. We end up with four vertices which hold the erase-triggered flag.

As we have an or-based refinement, erasing the vertices means that effectively only the three cells in the centre are coarsened. The other cells remain refined with a lot of adjacent hanging vertices.

Using the dynamic mesh refinement

Multi-action set usage pattern

In many applications, the refinement pattern is not known a priori. Instead, the action sets build up the knowledge where to refine or coarsen: They start with an empty std::vector< peano4::grid::GridControlEvent >, and push back events throughout the grid run-through. As action sets are not persistent in-between mesh traversal sweeps, as codes might switch between different action sets, and as clones one action set per subdomain (again, the number of subdomains per rank can change over time), we have to be careful with the data management.

A popular pattern is to have a static std::vector< peano4::grid::GridControlEvent >. In this case, an action set can build up a local set of control events, and commit them to the static set. The static set is then returned by getGridControlEvents() which consequently erases it to accept new events.

To make this work, you might want to work with two static sets: the currently active one and a new one, as each subspacetree will query getGridControlEvents() independently. However, we can exploit the fact that each subtree/subdomain asks for the grid control events before they actually trigger beginIteration(). So it is safe to hand out the static set and to clear it within the begin iteration.

If you work with multiple action sets and an algorithm which switches between the different ones, you will have to centralise the static control events. One action set might feed into the event, while the next one delivers from this centralised repository. Alternatively, you can add another (static) boolean which you set to true whenever getGridControlEvents() is invoked. The central events are then cleared by beginIteration() if and only if the boolean is set.

Parallelisation

Peano does not reduce the grid control events globally. That is, if you have multiple MPI ranks, you have to ensure they exchange their information with each other. If they don't each MPI rank will refine and erase their area independently. The mesh will still be consistent, as a vertex along a boundary which is refined will also trigger a refinement in the remote neighobur (or-based refinement policy), but there is no global data exchange. There is a routine peano4::grid::reduceGridControlEvents() that allows you to reduce information.

Refining the mesh

Due to the or-based refinement criterion, refine instructions tend to spread through the mesh quite quickly. I therefore recommend that you scale the refine command down, i.e. make it only cover fragments of a cell. At the same time, it makes sense to ensure that two cells which trigger a refinement also trigger two refinement events which are adjacent, as this allows peano4::grid::merge() to merge them into one larger refinenet instructions. So, as a rule of thumb, I usually recommend to make refinement events span a mesh size which is around 95% of a cell. The peano4::grid::merge() operation, by default, works with 10% inaccuracy and then is still able to merge refinement events triggered by adjacent mesh cells.

Coarsening the mesh

Coarsening a mesh is tricky, as coarsening areas have to span quite some cells to actively remove mesh cells. This is a natural consequence of Peano's "at least" policy. At the same time, you want a coarsening never ever to eliminate a mesh part that you want, as this might need to oscillations where you erase and refine and erase again, while it also should not be cancelled out by a refine event "accidentially".

To enable Peano to erase safely, I usually identify refine cells of which I want to remove the children, and then I trigger an erase event which has three times the side line of this very cell. That is, if a cell has the mesh size h, the erase event has the size 3Ch where the C is a value slightly larger than 1. I often use 3.1h overall. This means that a cell tells Peano "hey, please erase my children and the children of the neighbours".

Working with these extremely aggressive coarsening factors is important for refinement patterns which are non hexahedral, and it is important along domain boundaries, where we cannot hope that a neighbour concatenates their erase command to ours. Yet, while this will eliminate small refined patches that might have been left out or are close to the boundary, such an aggressive erase will leed to oscillations, as we might now ask for an erase over a cell which we actually wanna keep.

To avoid oscillations, you can introduce a "keep this mesh" event through artificial refinement instructions. Refinements overwrite erase instructions. Therefore, you can always trigger a refinement event for a cell which actually does not refine this cell any further (just make the event span the whole cell with the cell's mesh size as target mesh size).

Such a refinement event does not refine the mesh any further. However, it prevents any erase event to remove this part of the mesh. So it is effectively a "keep the mesh" instruction.

Optimisation

Consult the generic optimisation remarks for some details around performance flaws tied to dynamic mesh refinement.