 |
Peano
|
|
Peano
|
This section discusses some Peano-specific performance optimisation steps.
While Peano provides simplistic performance analysis features to spot some flaws, a proper performance optimisation would likely rely on external performance analysis tools.
If you plan to run any performance analysis with the Intel or NVIDIA tools, I recommend you to switch to the respective toolchain and logging before you continue. For other performance tools such as Scalasca/Score-P, Peano offers bespoke toolchains, too. These toolchains ensure that all tracing information is piped into appropriate data formats.
Most developers start with a release build for the performance analysis. However, you might want to switch the tracing on for a deeper insight. Consult Peano's discussion of Build variants. If you use tracing, you will have to use a proper log filter, as Peano's log information otherwise becomes huge, i.e. challenging to handle, and the enormous data quickly pollutes the runtime measurements. The data also might be skewed slightly due to measurement overhead.
Besides the trace option, Peano also offers a statistics mode where the code samples certain key properties. These statistics are meant to complement real performance analysis with domain-specific data: We think that it is the job of a performance analyis tool to uncover what is going wrong and the statistics then can help to clarify why this happens from an application's point of view.
Any optimisation should be guided by compiler feedback and proper performance analysis. For the (online) performance analysis, Peano provides tailored extensions for some tools such as Intel's VTune or the NVIDIA NSight tools. They are realised as bespoke logging devices.
If you want to use compiler feedback, we do routinely use the Intel toolchain. For them, the flag -qopt-report=3 yields useful feedback. However, running the whole code with compiler feedback yields a lot and lot of files. It also seems to slow the translation process down. I therefore recommend that you first find the observer class which invokes the compute kernel you are interested in. After that, create the Makefile (only once, as it will be overwritten). Within the makefile, alter the linker step:
You throw away the object file and then you rebuild this single file yet with the optimisation reports on.
Most successful vectorsation passes depend upon successful inlining (despite marking functions as vectorisable). To facilitate this inlining, you can either move implementations into the header, or you can use ipo. The following remarks discuss ipo in the context of the Intel compiler, but we assume similar workflows to apply to any LLVM-based toolchain.
The switch to ipo requires some manual modifications of the underlying Makefile:
Here is an example excerpt of a successful, modified Makefile:
The final ipo optimisation report will end up in a file ipo_out.optrpt.
We use the same geometric load balancing for both the MPI code and on the node. In the latter case, subpartitions aka subtrees are distributed over several threads. The load balancing can be written manually for your application, or you can use classes from the load balancing toolbox that is shipped with Peano.
The documentation of the load balancing toolbox contains some generic explanations why certain things work the way they do and what has to be taken into account if a code suffers from certain behaviour. It is important to read through these explanations prior to tweaking the load balancing as discussed below.
Before you continue, check if the individual trees are well-balanced. Do they have the same size? If not, you might want to study the remarks below on ill-balanced partiitons. Now, assume they are well-balanced. If you have a well balanced problem, the trees have all roughly the same amount of local cells:
All looks fine here. If you don't get any (reasonable) speedup, then you should look at the ratio between the total number of local cells and the total number of remote cells (granularity).
In the example above, we have 12 trees where each tree holds 19644 cells. Therefore, we have very good balanced load. Now, we look into the ratio of the total number of local cells (235737) and remote cells (33331):
In some heuristic measurements we deduced a "rule of thumb" where a granularity of greater than ~10 results in a linear speedup in a strong scaling setup (neglecting other effects like memory bandwidth, etc.). If you get a smaller granularity than ~10, you will lose performance (in relation to the hardware resources you throw at the problem) that worsens, the smaller the granularity gets.
To remedy this effect you will need to find ways on how to increase the granularity in your simulation.
Possible ways to do so can be:
Most of Peano's solvers (such as ExaHyPE) support tasking to facilitate light-weight load balancing. However, even the best load balancing will not be able to compensate for a poor initial geometric distribution. To assess the quality of your partition, Peano's loadbalancing toolbox provides a script that visualises the distribution of cells.
If the cell distribution is similar to the one above, you have subpartitions of significantly different sizes. In a profile, such an ill-balanced setup materialises typically in high task runtime spin times. In OpenMP for example, __kmp_fork_barrier() appears high up in the list of the most expensive routine. If you don't want to use the visualisation script, you can also check the program dump of your code.
rank:1 toolbox::loadbalancing::dumpStatistics() info 2 tree(s): (#1:13/716)(#3:14/715) total=27/1431 (local/remote)
is a proper load balancing for two cores, as we have 13 vs 14 cells. There are some generic ideas that you can try out:
It is important to keep in mind that all data displayed here on the terminal are geometric data. If you have a highly inhomogeneous cost, as you use kernels with varying workload (particles or non-linear solvers within cells), if you use task parallelism heavily, if you use adaptive mesh refinement, or if you use different localised solvers in different subdomains, then all the data here as well as the recommendations have to be taken with a pinch of salt.
See the comment above on the recursive top-down splitting. In this context:
Using the schemes that spread out immediately often makes the resulting domain decomposition quality worse, as they realise a greedy approach which kicks in while the grid is not completely constructed. In such a case, use a combination (cascade) of load balancing schemes, i.e. start with spreading and then use something fairer.
Before you continue, ensure that the individual subtrees are well-balanced (see comment above). Once you are sure that this is the case, a high spin time implies that the trees are simply too small. In OpenMP, this manifests in outputs similar to
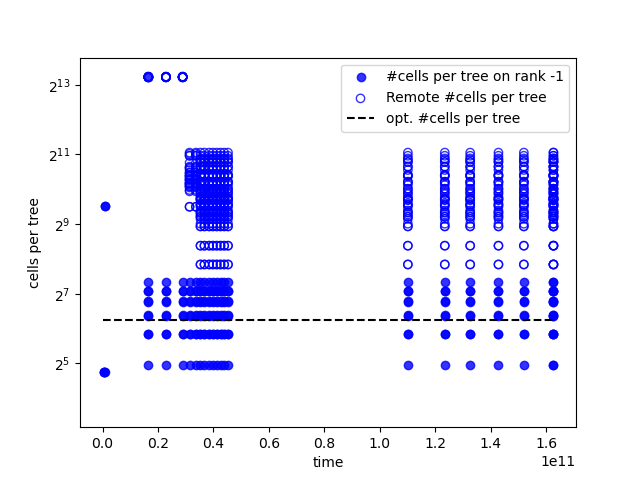
Once you dump the output into a file and you visualise it with the script enabling a display of remote trees, too small trees also usually manifest in very high remote cell counts, i.e. large numbers of outer and coarse cells, compared to actual fine grid cells. Use the flag –remote-cells. Below is an example where we have many trees per rank, and each tree hosts only a few local fine grid cells compared to total number of cells per tree:
This setup manifests in plots as the one below:
The real cells per thread (solid circles) are okish clustered around the optimum, but the remote cells (empty circles) are by magnitudes more. In this case, it might be wise to reduce the tree size and to remove the overhead in return.
Obviously, it depends on the load balancer that you use how to ensure that the number of trees is not too big. The generic load balancer toolbox::loadbalancing::RecursiveSubdivision for example accepts a configuration, and this configuration can pick a minimum tree size.
If you restrict your subtree/subpartition size, you run risk that you end up with a domain decomposition which cannot keep all cores busy. In this case, you have to increase the code's concurrency otherwise, i.e. not via geometric decomposition. Additional tasking within your code for example is an option, or compute kernels which themselves can use more than one core.
See general remarks in documentation of tarch::allocateMemory() and tarch::MemoryLocation.
Peano realises a strict cell-wise traversal paradigm, where individual actions are tied to single cells, faces or vertices. Therefore, Peano's AMR is also controlled by sets of refine and erase events. The decision to refine or erase a mesh is made by Peano by comparing each and every mesh entity against the set of erase and refine commands. This happens in peano4::grid::Spacetree::updateVertexAfterLoad().
If you work with thousands of mesh refinement and coarsening events, the AMR checks themselves become time-consuming. Therefore, each tree traversal invokes peano4::grid::merge() on the command first. This routine tries to consolidate many erase and refine commands into fewer ones, and it also throws away those erase commands which contradict refines. However, you can still tune this behaviour:
Peano supports both task-based and data parallelism. The former is specific to extensions such as Swift or ExaHyPE, i.e. each has their own tasking approach. There are some generic recommendations though, and we discuss them below. All Peano codes can support data parallelism by a textbook non-overlapping domain decomposition. Actually, we have a tree decomposition.
To enable a tree deccomposition, a load balancing scheme has to be activated. This makes Peano yield multiple trees and these trees are then either distibuted among ranks or among threads or both. Therefore, the generic domain decomposition tweaks and flaws are discussed in a section of its own above on data decomposition.
If tasks make your system slower, there can be multiple reasons:
This could be a sign of a scheduler flaw. Peano offers multiple different multithreading schedulers: It can map tasks onto native OpenMP/TBB/... tasks or it can introduce an additional, bespoke tasking layer. If your code becomes significantly slower (or even hangs) once you have increased the concurrency level, you might want to alter the scheduling. I recommend that you start with native tasking, i.e. a scheme which maps each task directly onto a native TBB/OpenMP/... task. For many codes, this disables them to offload many tasks to GPU or the balance between grid traversals. However, a native tasking is a good starting point to understand your scaling and the also plays along well with mainstream performance analysis tools.
This could either be a scheduler flaw, or you have too few enclave tasks. The scheduler flaw is discussed in Peano's generic performance optimisation section, but ExaHyPE offers a special command line argument to switch between different tasking schemes. Run the code with help and use
--threading-model native
or another option afterwards to play around with various threading schemes.
If this does not work, switch to task-based kernels.
Validate if both ranks get roughly the same number of cells. If this holds, the performance drop is due to a bad per-rank (shared memory) load balancing most of the times. Study the recommendations above after you have visualised the distribution of the cells per rank.
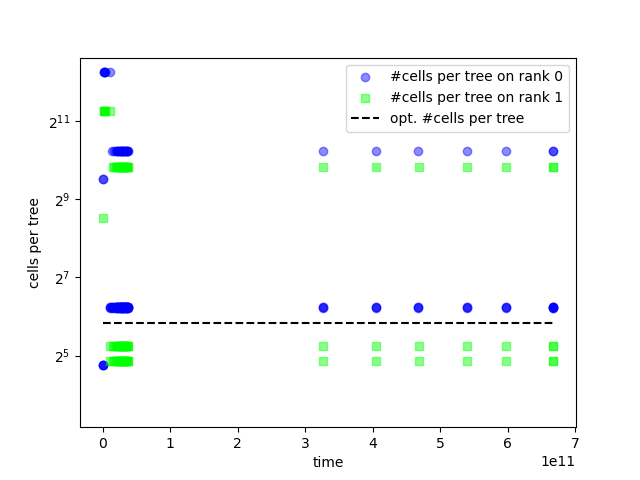
The example above results from outputs as shown below:
We have 41 or 49 trees, respectively, on a single rank. While this might be reasonably balanced, we have 64 cores/threads per rank and hence can conclude that our load balancing does not keep all cores busy. We loose out on threads. Enclave tasking and parallel compute kernels can, to some degree, mitigate this problem, but we should aim for a proper work distribution right from the start, i.e. geometrically. Further to our observations so far, we see that rank 0 is significantly heavier in terms of total cell count.
What we furthermore see from the logs (as well as from the plot) is that each rank has one massive tree, and then a lot of smaller trees. The smaller ones are all properly balanced, i.e. they are all of the same size (around 75 on rank 0 and around 38 on rank 1). But then we have this one massive tree besides these small ones. That is not a good load balancing, and - if you use OpenMP - will manifest in high spin times per node:
In this case, we observe that the individual rank has made a reasonable load balancing decision once it has "recovered" from the global spread out over all ranks:
However, while the load balancing (rightly so) decided to keep all cores busy, it seems that not enough cells had been available at the time to bring them into the business. Study the single node load balancing discussion above.
1.9.1