|
Peano
|
|
Peano
|
A summary of how Peano runs throug the mesh and builds up the active and local sets which are then used to realise particle-particle interactions.
Peano realises mesh sweeps via tree walkers, i.e. automata which run through the tree top down and then bottom up again. Each algorithm step equals one complete mesh traversal of all mesh resolutions. Throughout this traversal, the automaton triggers events (or observations) that are then mapped onto action sets.
While running through the mesh, i.e. spacetree, the automaton maintains different particle sets. For the construction rules, it is important to keep in mind that vertices of any level hold only particles whose search radius is stricly smaller or equal to the corresponding mesh size. Particles with a large search radius are consequently stored on coarser levels. This allows us to define our particle sets:
The illustration below shows two levels of a spacetree with bipartitioning (although we use tri-partitioning in Peano). There are eight particles in this example. The tree automaton is currently in the finer, dark blue cell and triggers touchCellFirstTime().
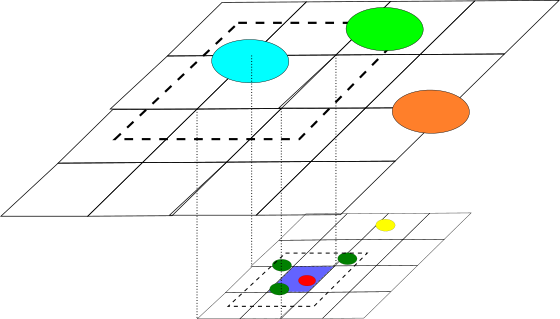
We need the local and active sets to cover an area that is bigger than the actual cells, as we want to capture all particles of this level that might theoretically interact with the particles located within the cell.
If you want to update particles within a cell, you should introduce a boolean per particle that indicates if you have already touched it or not. The particle-to-cell association is not unique: isContained() has to work with a slack, as it deals with floating point numbers. If a particle resides on the face between two cells, it hence is contained within both cells. You might update it twice if you work within touchCellFirstTime() or touchCellLastTime(). I therefore recommend to add a boolean per particle which highlights if a particle has already been updated.
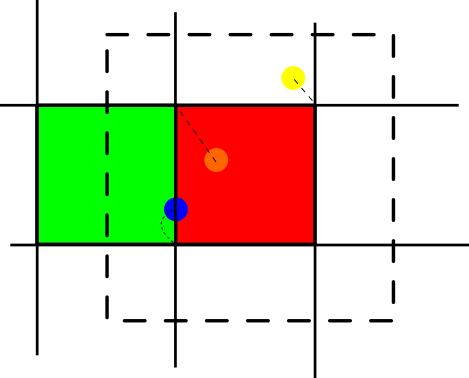
The illustration above highlights the problem: The blue particle sits exactly on the face between two cells. It is associated to the bottom vertex (dotted line). When we update it within the red cell, we will later on also update it one more when we hit the green cell. So we need a marker. Most codes unset this marker in touchVertexFirstTime() for all local particles, so it is properly initialised. The update then sets the marker to keep books which particles have been updated and which haven't.
If you want to update particles of a cell due to particle-particle interactions, you should only update particles which hold the right value of the corresponding flag plus whose centre is within the cell: Particles belong to the local sets of up to \( 2^d \) surrounding vertices. If you want to update the red particle vs.~the green one left above it in the sketch above, it becomes immediately clear that the green particle will be in the local set of this cell, but also in the local set of the cell left of it and also the one left above it.
is your friend. We illustrate this above by means of yellow particle which has an impact on the orange particle. We can update the orange particle with the impact from the yellow particle when we hit the red cell. However, the orange particle is also in the local set of the green cell. If we updated the orange particle there, we would miss the yellow one.
As the local particle set is a subset of the active set, you will compare a particle to itself if you simply compare the particles of the active set against the particles in the local set. This requires an additional if in most kernels.
All of these remarks do not apply if you work within touchVertexFirstTime() or touchVertexLastTime(). Here, the set of particles associated with the vertex is unique. However, you cannot compute any proper particle-particle interaction here, as you don't have the active sets of the neighbouring vertices.
Our scheme at the moment does not provide any means to exploit force symmetries between cells. However, you can tailor compute kernels to exploit any symmetry you want.
If particles can only interact with their level, you can use peano4.toolbox.particles.UpdateParticle_SingleLevelInteraction or peano4.toolbox.particles.UpdateParticle_SingleLevelInteraction_ContiguousParticles. Both types differ in their assumptions of how the particles are organised in memory. Other than that, their realisation is rather straightforward:
As particles are tied to vertices, we know that a particle has not been read prior to the touchVertexFirstTime() for the corresopnding vertex. We let touchVertexFirstTime() imply an event alike touchParticleFirstTime(). If a cell is hit, we know that all of its vertices have been read, and therefore all of its particles have been. After we have touched a vertex for the last time, we also won't access its particles anymore.
Each particle has an attribute getCellH() which provides the user code information about the cell currently holding the particle. That is, whenever one of the update action sets moves particles up or down in the mesh hierarchy due to particle state changes or adaptive mesh refinement, it will automatically adopt the cell h.
We can exploit this property to implement valid multiscale interactions: If two particles L (local) and A (active) are on the same grid level, we evaluate A-B and B-A separately, i.e. once draw A from the local set and B from the active set and then the other way round. That is, we evaluate a function \( f(L,A) \), knowing that \( f(A,L) \) will be done later in the neighbour cell, e.g. Notably, we do not exploit
\( f(L,A) = -f(A,L) \)
and similar relations, even though they are omnipresent in Lagrangian formalisms.
The assumption that the counterpart will be taken care of is wrong if A resides on a coarser level than L. Local particles see all (active) particles from coarser scales, but coarse scale data doesn't see fine scale data. So if the particle's cell size \( h(A)>h(L) \), then we have evaluated \( f(A,L) \) immediately as well within the loop. If we evaluate \( f(A,L) \) for \( h(A)=h(L) \), it will be evaluated twice - which is bad if the evaluation feeds into an accumulation.
The construction of the active and local sets works if and only if the particles are correctly assigned to mesh vertices. That is, they have to be stored within their closest vertex on the right mesh level in line with our storage conventions.
The very moment you alter a particle position, you might violate the correct assignment. From this point on, the local and active sets are corrupted, i.e. might hold too many particles or miss a few. Most codes equip the particles with markers (updated) and do not move particles directly. Instead, they maintain two positions - the current x and a xNew - and then copy the xNew over into x when a vertex is touched for the last time. This way, the local and active sets deliver correct snapshots of the system described by x and are hence correct.
Once we have assigned particles a new position (or a new search radius), we have to re-sort them. This is required to preserve the particle-mesh consistency. It is important to keep in mind that particle sorting requires at least two mesh sweeps. That is, once you change a particle position, the new valid particle-vertex association might not be in place in the next mesh sweep. Therefore, the active and local sets might be corrupted in the next sweep. They will be fine once all drops have finished. This fact requires some further attention:
If a particle has changed its position or search radius in mesh sweep n, it might not be assigned to the correct vertex anymore. Some particle sorting (cmp discussion of variants in Sorting: Preserving the mesh-particle data consistency) might be able to handle some of these cases, i.e. put some particles straight into the right vertices, but all sorting approaches might run into situations where they have to lift particles to the next coarser level. In the iteration n+1, a particle hence might reside on a coarser level and will be dropped. However, if we plug into touchCellFirstTime(), these drops have not yet happened. That is, the particle currently resides on the wrong level and consequently messes up our active and passive particle sets.
There are work-arounds. For example, you can check via
that you don't double-count particles. However, at the end of the day it is all a mess. If you need particle-particle interactions after a move, insert some "empty" mesh traversals to get the sorting right.
Here is an illustration what can go wrong:
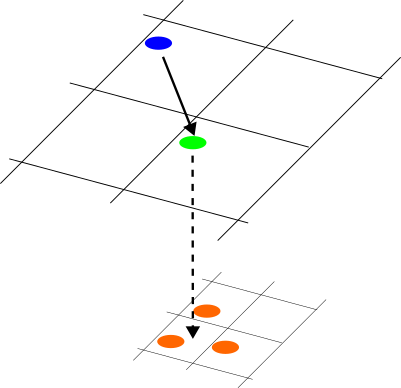
The blue particle has moved into the green position in mesh sweep n. In mesh sweep n+1, we hit the cell in which the blue particle (now green) has ended up. We construct the active set and have no other interacting particles. So we should not update it. That is what the if statement using particleWillBeDroppedFurther() is for. Instead, we handle whatever we do on the refined coarse cell, ignoring the particle, and then descend. Throughout the descend, the particle will be dropped onto the next finer level. Now, the dropped green particle will see the orange neighbours.
Checking particles with
can be very problematic along AMR boundaries, and peano4.toolbox.particles.api.AbstractUpdateParticleGridAssociation discusses these effects in detail using the arrangement below:
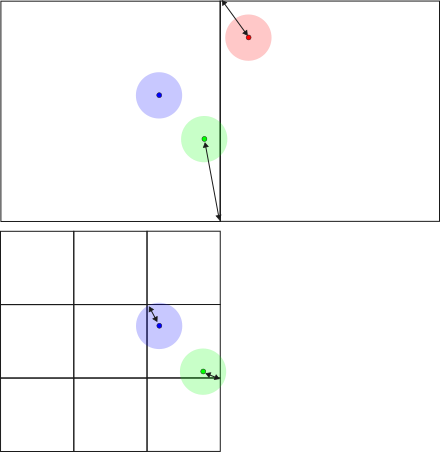
The problems arise for particles associated to the coarser level which you might want to sort into a hanging vertex on the next finer level. We never sort into hanging vertices, and this leads to the observation that multiscale interactions are mandatory in Peano even if you work only with the finest level logically.
The page Sorting: Preserving the mesh-particle data consistency discusses various aspects of this sorting and how it helps to keep the mesh-particle assocations consistent.
The particle toolbox offers two flavours of both type of particle interactions:
For all of them, particle sets are not persistent, i.e. they are built up on-the-fly. Yet, the realisation can make certain assumptions about their memory layout. These assumptions are discussed on a subpage of the Realisation details.