This page will frequently refer to action sets and their order. It therefore is reasonable to study the description of action sets first.

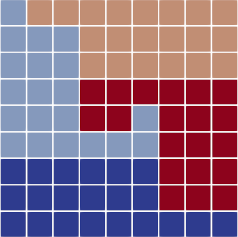
Peano starts from spacetrees and thinks in whole trees and only supports two types of decomposition operations: a split and a join. At the same time, it does not distinguish shared memory and distributed memory parallelisation. It only thinks in terms of trees. The trees and their traversal can either be deployed to ranks or threads or combinations of the two.

This statement is only weakened once you work with 's task interface. If trees issue tasks, then these tasks team up with the tasks handling the individual spacetrees. Your task graph starts to contain a mixture of tree tasks and user-defined tasks. This section discusses solely the tree decomposition aspect within Peano, i.e. ignores that there might be tasks as well.

Each subtree is completely independent: If Peano cuts a tree into chunks, these trees do not share any data anymore, no matter whether they are deployed onto separate ranks or separate treads or a mixture of those. We work with a multiscale, non-overlapping domain decomposition.

Domain decomposition within a (typical) Peano application

A tree in Peano is split along the Peano space-filling curve. This implies that the decomposition on each mesh level is a non-overlapping decomposition where each cell is assigned to exactly one chunk.

The illustration above makes this point: The blue and the red tree own a part of the overall domain. They do not share any cells, but they have a common boundary of four edges.

Data on these edges is replicated, i.e. the four faces exist twice: once on the red and on the blue tree. Also the two marked vertices exist twice.

Peano still works with proper trees and will actually let the red tree store parts of the blue partition as well and vice versa. How this is done is hidden from the user. Effectively, you know that each rank will somehow run through a part of the global domain. Some synchronisation and consistency rules remain in place:

Red will definitely skip all blue cells even if it should hold them.
Both trees will preserve the exactly same order for all shared data. If red touches the green vertex prior to the red one, then the blue partition will also process the vertices in the same order.
After each mesh traversal, the two trees will exchange their data (although there are two other data exchange schemes as well).
Both trees will trigger the related additional merge actions as described below.

Observers and action sets

If you run Peano 4, you buy into a SPMD paradigm, i.e. every single rank hosts one instance of Peano. Each Peano instance in return hosts multiple subspacetrees, i.e. multiscale domain partitions. When you pick a new observer with some action sets and you call traverse(), you expect that all the trees on each and every rank run through their mesh and use the same observer, i.e. deploy events to the same action sets.

It is the user's responsibility to ensure that the ranks do coordinate with each other. That is, the user has to ensure that whenever you run a certain type of grid sweep on one rank, then the other ranks run this sweep as well. I provide remarks on this at the end of the page. Most users will never ever see this part - notably not if they use high-level toolkits built on top of Peano such as ExaHyPE or Swift 2. The main codes produced by these high-level extensions automatically guarantee that all ranks do exactly the same.

Lifecycle of action sets

Each action set (instance of the class) is created once per tree. In addition, a prototype action set does exist.

In the baseline version, only one instance of an action set does exist per rank. For this action set, we call prepareTraversal(). Once this routine has terminated, we create N clones of the action set object if we host N subtrees. As ranks can host different numbers of subtrees, the number of clones differs per rank.

As each subtree is completely independent of all other subtrees, beginTraversal() and endTraversal() are called on the clone, i.e. multiple times. If vertices or faces sit exactly at the interface of subdomains, they their touchVertexFirstTime() is called multiple times, i.e. once per instance of this vertex. touchVertexLastTime() and the face events follow analogously.

After all trees on a rank have finished their traversal, i.e. all the endTraversal() calls have returned, the clones of the action sets are destroyed, and we all unprepareTraversal() one final time on the vanilla/baseline instance of the action set.

Data exchange

After the traversal has terminated, Peano is responsible to exchange all data. This is completely hidden. At one point prior to the next usage of any data, Peano will issue additional merge routines, so users can define domain-specific logic:

Event	Semantics	Dependencies
receiveAndMergeVertex	If a vertex exists on N different trees, this routine is called N-1 times per tree, i.e. in total N(N-1) times: Each local vertex is presented its N-1 counterparts per traversal.	This routine precedes touchVertexFirstTime().
receiveAndMergeFace	If a face exists on two trees, this routine is called once per tree, i.e. twice in total: Each local face is presented its counterpart per traversal.	This routine precedes touchVertexFaceTime().
----------—	----------—	----------—
touchVertexLastTime	Afer this routine has terminated, each tree takes (for all vertices along a boundary) the latest version and shares it with all other replicas. It sends it out. The sent data will be presented to the merge routine on the counterpart at an arbitrary time in the next mesh sweep.	This routine precedes receiveAndMergeVertex of the next mesh sweep.
touchFaceLastTime	Afer this routine has terminated, each tree takes (for all faces along a boundary) the latest version and shares it with the other tree holding a copy of this face. It sends it out. The sent data will be presented to the merge routine on the counterpart at an arbitrary time in the next mesh sweep.	This routine precedes receiveAndMergeFace of the next mesh sweep.
----------—	----------—	----------—
prepareTraversal	Is called once per rank before we create the actual action sets.	Precedes the beginTraversal() calls which are called once per subtree.
unprepareTraversal	Is called ocne per rank after the rank-local traversals have all terminated.	Follows the last endTraversal() call.
----------—	----------—	----------—

Decomposition constraints

Before we discuss any algorithms that Peano employs, it is important to state that Peano always commits to two fundamental constraints:

Topology constraint Also Peano's coarser cells are uniquely assigned to one tree. Between the ranks, we have a tree topology again. That is, a splitting of a tree is always realised such that there's a unique master-worker topology.
Grid regularity constraint Peano implements one further constraint which refers to the handling of AMR. A cell can be forked onto another rank if and only if all of its vertices are persistent.

Both constraints are implemented via peano4::grid::Spacetree::isCellSplitCandidate(). Details on this as well as further rationale (the ones below refer to the constraints only) can also be found in peano4::grid::Spacetree::splitOrJoinCellBottomUp() and peano4::grid::Spacetree::splitCellTopDown(). As we have to accommodate these two constraints, splits typically never are "exact", i.e. you might ask for 100 cells cells to be split off, but Peano will eventually only split off roughly 100 cells. It will try to stay close to 100, but the constraints have a higher priority than your request.

Load balancing schemes make recommendations to Peano how to split up the mesh. However, a split() call is never strict, i.e. Peano might decide to ignore it or to implement it only partially. This happens whenever the mesh changes on-the-fly or a constraint might be violated if we followed the split instruction strictly.

Examples

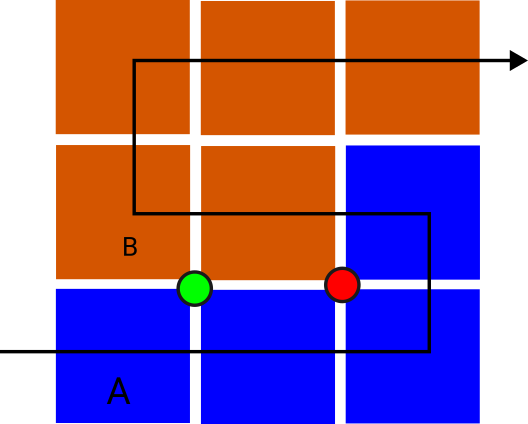
Some examples in the figure above sketch the implications of the topology constraint: In the left example, the yellow tree has split up into yellow and green. The green tree has further split into green and red. The code usually tries to keep whole trees, i.e. children and parents, within one tree. In the left example, it would be natural to make the very right green cell on the first child level a red one, too. This way, a whole tree would reside in red. However, if we made this single cell red, then red would become a child of yellow, i.e. we would change the rank topology. Peano never does so. In the right example conversely, I've asked the yellow tree to split into yellow, green and red in one rush. This time, the right level 1 cell becomes red already.

Both examples show that a split of one tree into further trees never results in the fact that the original tree becomes empty. Otherwise, we would again change the tree topology upon the ranks.

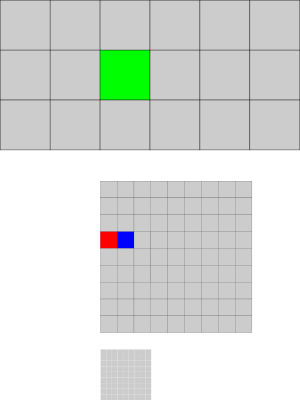
Im the mesh above, a rank can fork off the green cell. In the sketch, the green cell is the root of a tree with two more levels. A fork of the green cell consequently would fork off a whole tree (see topology constraint above). However, we are forbidden to fork off the red cell and its nine children. We could fork off the blue cell, but the red cell is hanging and therefore not a split candidate. It is, in general, difficult to identify such critical situations: The green cell with all of its children can be identified in a top-down sweep, but then we run risk that the green cell plus its children sum up to more cells than we actually wanna split. Therefore, we provide two split variants (cmp peano4::grid::Spacetree::splitOrJoinCellBottomUp() and peano4::grid::Spacetree::splitCellTopDown()) and leave it to the user to decide whether they want to try to meet the number of cells split off or try to maximise the probability that whole trees are split off.

Rationale

We want to work with a proper master-worker topology such that we have well defined relations where a tree has to send data to if data has to go to coarser levels. The topology also allows us to run reductions along trees, or to clarify who is allowed to split and who is not. The topology furthermore allows us to veto erase commands if they would erase whole subdomains. Most importantly, a clear master-worker topology makes joins more straightforward (they are always nasty), as we don't have to deal with 1:n data flows when we join a partition.

The regularity constraint is important as we have to update a vertex state if a mesh refines or erases dynamically. In this case, a rank might trigger an erase and a child who holds the neighbouring refined cell has to implement this erase as well. If the erase now suddenly creates a hanging node on the coarsest level, this hanging node does not carry any adjency information anymore. Adjacency now has to be propagated through from even coarser level, which is difficult in a distributed data environment. By defining that all the coarsest octants on a rank have to have exclusively persistent vertices, we avoid the complications that adjacency information might be outdated. We also ensure that we handle all data consistency through (multilevel) exchange of vertex data with neighbours. No data has to be propagated between levels just to get the vertex data right.

Data flow patterns

With these two constraints in place, we can discuss Peano's data flow: The code relies on a multiscale non-overlapping domain decomposition. Within the trees, we distinguish three different types of parallel data flow:

Horizontal data exchange is exchange between two cells of one level along their boundary.
Synchronous vertical data exchange is exchange between trees where one resolution meets the other. Vertical data exchange is synchronous if a coarse mesh passes information down the grid hierarchy in one sweep and/or receives information from finer meshes and immediately, i.e. in the same sweep, continues to process these data. Synchronous vertical data exchange is used to stream data from one rank to the other if we fork.
Asynchronous vertical data exchange is exchange between parent-child trees where the coarser parent sends data to its child, but the data is used there on the child's coarsest level in the subsequent grid traversal. Along the same lines, we speak of asynchronous vertical data exchange if the coarest level on a child sends data one level up, but these data are not used on the next coarser level which is owned by the parent before the next mesh traversal.

Horizontal data flow

Peano uses a non-overlapping domain decomposition. Therefore, ie shares/exchanges faces and vertices between different trees where these grid entities have adjacent octants on the same level which are owned by different trees. However, it never shares cells of one level. I explain the code's data exchange pattern with vertices. Yet, the same pattern holds for faces, too.

After a code has read/written a vertex for the very last time throughout a traversal, it sends a copy of this vertex away. In-between two iterations, all trees exchange their data. That is, in the next iteration any sent out data is available on the destination rank and can be merged into the local data structures. This merge happens on the destination prior to any other operation.

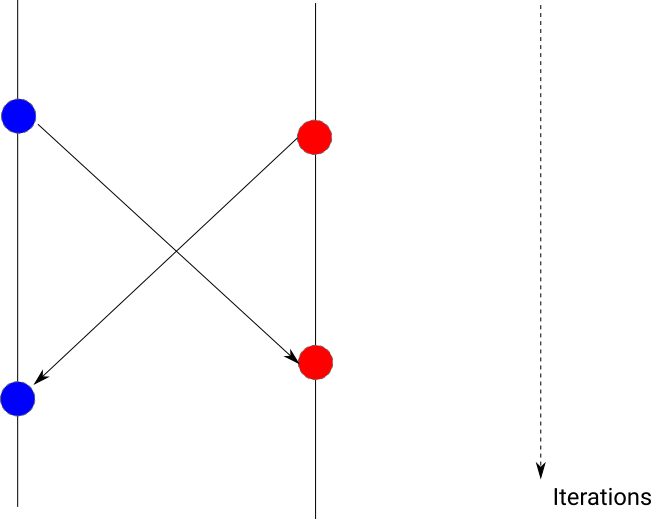
Peano consequently realises a data exchange that is similar to Jacobi smoothers: Whatever you do on one tree won't be visible on the other trees in this very tree traversal. Prior to the next tree sweep, this information however becomes available there.

Asynchronous vertical data flow

This yet has to be written.

Synchronous vertical data flow

This yet has to be written.

Splits

Splits are triggered via peano4::parallel::SpacetreeSet::split(). Whenever you split a tree, Peano creates the new trees (either as threads on the local node or remotely via MPI). Each new tree receives a whole copy of the original tree. This includes both the core tree data and the user data. Once the tree is replicated, the individual trees start to coarsen. If they are not responsible for tree parts, they successively remove this part. After one or two iterations, each rank thus really works only on local tree. Due to this approach, splits require significant memory temporarily. It thus might be convenient not to split a tree too often in one rush.

Peano uses information from the actively used data to decide which data to replicate. If you have cell and vertex and face data but you use some of these data only in some substeps of you algorithm, please ensure that those steps that trigger the domain decomposition and those that run immediately after this do use all data types. Otherwise, Peano can't know what data is to be replicated when it splits trees.

If you split a tree, the original tree, i.e. the source of the data, makes the new tree run through two states: split triggered and splitting.

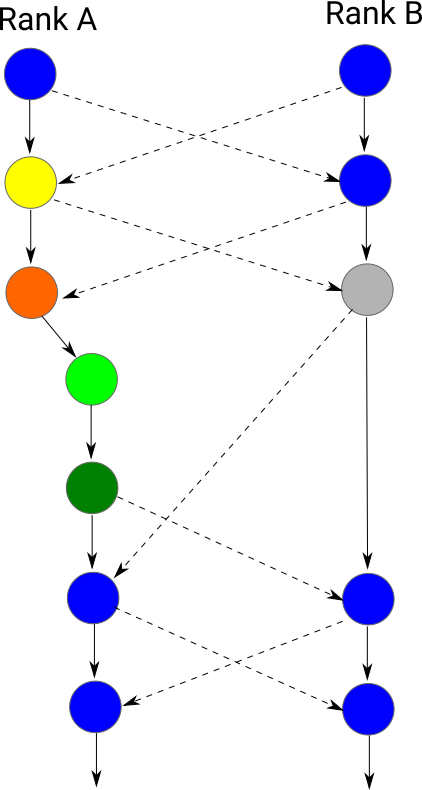
In a usual run, Peano's trees do exchange data in a way similar to the Jacobi smoothing: Each tree traverses its domain and sends out all boundary data. I call this horizontal communication as it is data exchange between non-overlapping domains which can be arranged on one grid level. In the next iteration, the data from neighbours has arrived and can be merged in. We obtain a criss-cross communication pattern (blue steps) where an iteration feeds into the neighbour's iteration n+1.

While a new id is booked by one tree if a split is triggered, this new tree does not yet physically exist. The original (source) tree keeps the complete ownership of all data, i.e. it does all refines and coarses and also creates all events. However, it already enters the new, yet to be created, tree's indices into all adjacency lists with are consequently sent out to the other ranks. This is the yellow step above. After the grid sweep, we mark the new tree id as splitting. At this point, all neighbours continue to send to the original tree, as they are not yet aware of any domain partition updates.

While an id is associated with splitting (orange), we know that all the other trees around start to send data to the new tree that is yet to be created: they receive the information about the updated adjacency and can send out their stuff to the new tree. Which does not exist yet (grey).

So the splitting rank (orange) traverses its domain and invokes all events. It has the semantic ownership. It merges in all boundary data from neighbours, but is does not send out the boundary data (anymore). After the splitting tree traversal has terminated, we establish the new tree by duplicating all the local data. This includes the user data, too.

The new tree (light green) subsequently is traversed once as empty tree. That is, all data travel over the stacks, but no events are invoked and no communication is happening. The purpose of this empty traversal is to get all data inot the right order.

Once the empty traversal has terminated, we run over the new tree again. This time, we label it as new (dark green). While we still do not invoke any event, we now do send out data. This is the sole purpose of the new traversal.

It is not guaranteed that the splits are all successful. See the routine peano4::grid::Spacetree::isCellSplitCandidate() which identifies cells that can be split. Effectively, you might call split and not get any tree decomposition at all.

With the information of the data flow above, any splits actually has to be realised over two grid sweeps which internally decompose into substeps:

The user asks a tree to split. From hereon, we have a master with some neighbours and a worker. The latter does not physically exist yet.
The master runs through its domain and tells all neighbouring ranks that the new tree will drop in in the future. At this time, these neighbours are not yet aware of the split (the information becomes only available in the subsequent iteration), so they continue to send their stuff to the master even though it might be vertices which will, in the future, belong to the new worker. We say that that we have a split-triggered in this iteration.
In the next iteration, the master is splitting. It still holds the ownership of all the data, as it receives for example all neighbour data. However, in the splitting phase, the master already sends out data to the worker where new domain boundaries will arise—even though the new worker does not exist yet. The same happens to all the neighbours. They send out boundary data to this new worker that will now enter the game.
Once the master has terminated, the responsible rank issues a couple of postprocessing steps:
1. It clones the whole master tree. This is only the grid structure, but it is a complete clone.
2. It instantiates the new worker with this cloned data. As we clone after the master's traversal has terminated, a lot of trees have already sent data to the new worker that we just cloned. However, this worker has not yet sent out any data, so we've broken the symmetry of our data exchange. Therefore, we run through the tree once as empty tree. In this sweep, we do nothing. We only run once through the tree to ensure that the stack data is in the right order.
3. Immediately after that, we do a new tree sweep. This sweep does not invoke any user events. It however sends out the data the others expect from us.

User data throughout splits

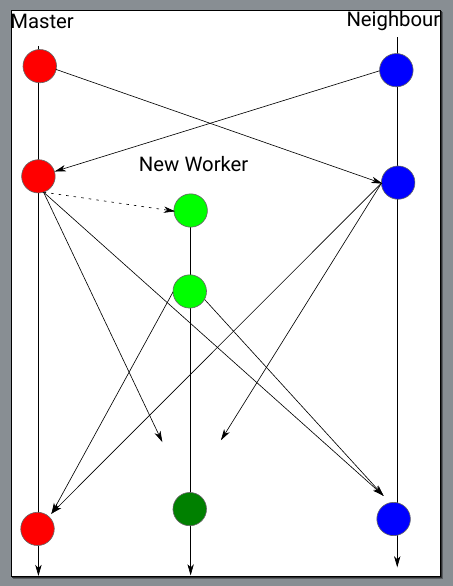
There is no need for the user to implement something manually, as long as the user ensures that the grid observer replicates the master tree on all new workers. The SpacetreeSet offers a function to do this automatically.

Data ownership throughout splits

Throughout the split traversals, the code continues to interact with the user and continues to compute, i.e. all splitting is seamlessly interwoven with standard compute mesh traversals. Throughout the whole split, the logical ownership of all data resides with the master, i.e. it is the master automaton who asks the user code what operations to invoke on the data.

Observation and best practices

As preserves the logical topology between trees, it is reasonable to strive for as wide tree topologies as possible. Otherwise, your meshes (coarsening) are very constrained. That is, it is better to split a tree a into five parts a,b,c,d,e with b,c,d,e being children of a rather than splitting a into b,c and then b and c again.

Joins

Joins are completely hidden from the user, i.e. there's no way to actively join trees. To understand why Peano issues joins from time to time, it is important to define vetoed coarsening.

Peano vetos any coarsening, if removing some parts of the grid would affect a child or alter the tree topology of the ranks. If a coarsening is vetoed, Peano remembers this veto. As soon as a rank whose master is affected by a veto hosts a tree cell which is unrefined, it joins/merges this cell into the master.

Vetoed coarsening typically does delay any grid coarsening. You ask for a coarsened grid, and it first of all applies this coarsening to all ranks that have not decomposed further. Once these have finished their coarsening, it joins those ranks that stop further coarsening into their master. Once this is complete, it continues to coarsen. This process can continue recursively.

For this reason, the join of partitions in follows a few mantraic principles:

We only join partitions if they do not hold refined cells. We call such partitions deteriorated (in a tree sense). If a partition holds a refined cell, it cannot be merged into its father.
We hide joins from the user, i.e. a user can split up a partition and thus implement load balancing, but a user is never allowed to join. Joins are always triggered by 's core internally. The policy is as follows:
- We join a deteriorated partition if the master resides on the same rank and if this master would like to coarsen its domain but can't do so as this coarsening would violate the tree topology (see dicussion above).
- We join a deteriorated partition if the master resides on a different rank. The idea here is that such deteriorated partitions always induce quite some overhead.

There's technical rationale behind some items: We don't join deep trees with their master as both master and worker work with their LET, i.e. try to coarsen their respective mesh as aggressively as possible after the split. Therefore, a master does not have all grid infrastructure of a worker available. It would require some complex zipping to bring the info of two trees together. If I realise a deteriorated-trees-only policy, I don't need such zipping as (almost) all information is available on the master already.

Temporal ordering throughout joins with SpacetreeSet

Analogous to the splitting process, each join is broken up into two traversals. Throughout these traversals, the code continues to interact with the user and to compute. In the first traversal, the worker tells everybody else that it intends to join with its master. However, nothing happens. Throughout this first traversal (join-triggered), all the neighbours of a rank as well as its master continue to send boundary data to the tree that intends to join, as they are not yet aware of the join intention.

In the second traversal (joining), we distinguish two steps. First, the worker traverses its domain. The traversal of the master is postponed. Throughout the traversal, the worker receives incoming data and merges it with the local information. Information on the grid topology is immediately streamed to the master. Immediately means after the vertex data is read for the first time and merged. See the discussion on the grid data below. After that, the worker continues, as it still own all data (see below). When it writes data to its output stream for the very last time, the data that is adjacent with the master is written to an output stream.

In the second step of the second traversal, the master now runs through its grid. Before that, both grid and user data from the worker are streamed in. The master takes the streamed in mesh data right after it has read its information. Whenever it runs through a mesh entity for the very last time, it merges its local user data with the streamed-in records from the (former) worker.

Data ownership throughout joins

Throughout the split traversals, the code continues to interact with the user and continues to compute, i.e. all splitting is seamlessly interwoven with standard compute mesh traversals. Throughout the whole split, the logical ownership of all data resides with the master, i.e. it is the master automaton who asks the user code what operations to invoke on the data.

Grid data streaming throughout joins

In principle, one might assume that no streaming is required if we merge only deteriorated trees. After all, if a rank deploys some subtree to another worker, it still holds its root node locally (though flagged as remote). However, there's one delicate special case: If a tree joins its master and another neighbour changes something within the mesh, too (merges as well or splits up), then the master won't be notified of this info. The update information will reach the worker while it is joining into its master. Therefore, a merging worker does stream its vertex data immediately into the master while it joins. This streaming requires us to break up the join process into two distinct traversal phases (see primary vs. secondary remark above).

We don't have dedicated streams in , and there's no communication channel for joins either. However, there's by default for any piece of data a vertical exchange stream. For the joins, we hijack the vertical stacks and write the data to them. When we hand the data over to the master, we revert the order on the stack and thus effectively convert it into a stream.

User data streaming throughout joins

This section is incomplete and only partially implemented.

Hijack vertical stacks on grid side!

The realisation of joins and splits in is totally asymmetric: For a split, all data of the splitting tree is replicated and then both the original tree and its new worker coarsen the partitions they are not responsible for. This process is realised through two additional traversals on the worker side.

Throughout the join, no data flows logically, as the master already has the mesh. Furthermore, only data that is actually owned by the worker is handed over to the master.

All the trees on one rank are held within one instance peano4::parallel::SpacetreeSet. The set is actually a singleton, to you don't have to ensure manually that there is only one set on your rank. You can tell the spacetree set to decompose one of the local spacetrees further through its split() routine. If you invoke its traverse() routine, it will automatically ensure that all spacetrees do the same, though the actual travesal of various trees (aka subdomains) will run in parallel on multiple threads.

Implementation

Using replication information

Sometimes, you have to know how often a vertex or face is replicated. If you compute the global residual of a linear equation system for example, you likely would like to accumultae this information in touchVertexLastTime() or touchVertexFirstTime(). However, this means that you consider faces and vertices at domain boundaries multiple times.

For faces, you can simply check if a face is at the parallel boundary. For this, peano4::datamanagement::FaceMarker provides you the routine peano4::datamanagement::FaceMarker::isAdjacentToParallelBoundary(). For vertices, the equivalent is peano4::datamanagement::VertexMarker::getNumberOfAdjacentTrees().

Distributed memory (MPI) realisation

A typical Peano4 code distinguishes the global master (rank 0) from the workers (all other ranks). The global master hosts all the program logic, i.e. decides which steps to run in which order. There's no reason for you not to emancipate from this pattern, but it has proven of value. The main of a Peano 4 application therefore always looks similar to

if (tarch::mpi::Rank::getInstance().isGlobalMaster() ) { 
  // All the program logic, i.e. all decisions here else
}
else { 
  // React to rank 0's decisions what to do next on all ranks
}

Before we start, lets assume that each individual step (type of run through the mesh) has a unique positive number.

Peano handles all (multiscale) boundary data transfer and data migration within the mesh. Everything not tied to the mesh is not handled by Peano. That means there's not even a reduction of the grid statistics over MPI. We do provide reduction and broadcast features however. If you need these global data, I recommend that you realise all reductions and broadcasts in your main rather than inside of the Peano mappers or other classes. See the discussion at MPI programming.

Shared memory between different trees (instances of action sets) and different action sets on one rank

This section discusses shared memory programming from a domain decomposition view. More general remarks on shared memory primitives and task-based programming can be found in the discussion of the tarch::multicore namespace.

Realising global variables shared between action sets is in principle impossible: Action sets are not persistent. They are created per traversal per tree. Furthermore, you have absolutely no knowledge how many trees any rank hosts. The only thing you know is that all trees will kind of start their traversal around the same time.

However, nothing stops you from having a singleton data or static data set somewhere and to let all action sets write into this one. You just have to ensure that you protected writes with semaphores.

If a lot of action sets all hit the same static data concurrently, you get a lot of lock overhead. In this case I recommend that each data set creates its own local data and reduces all information from its tree there. In endTraversal(), you can then lock the static global data and commit your data there before the action set is destroyed.

Design patterns for (MPI) global variables between action sets