|
Peano
|
|
Peano
|
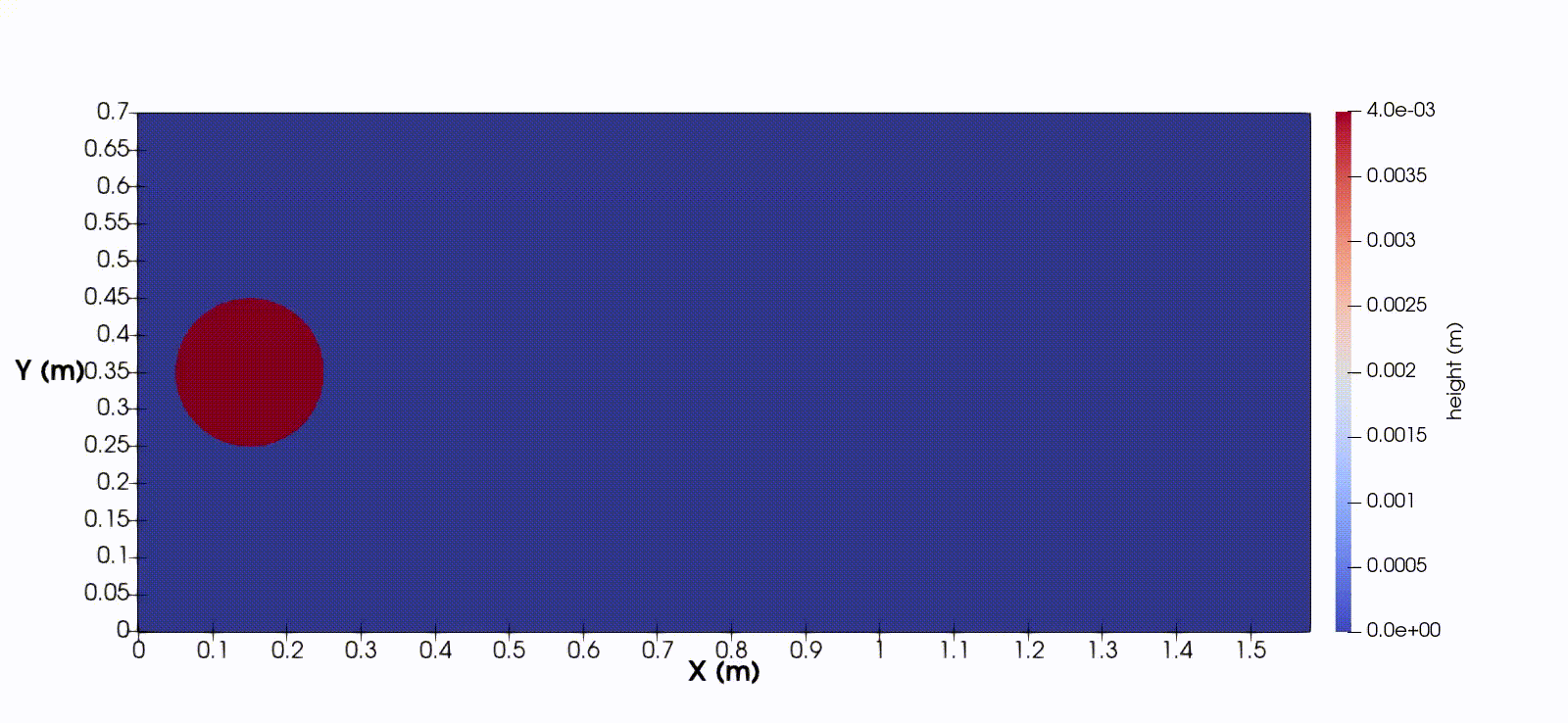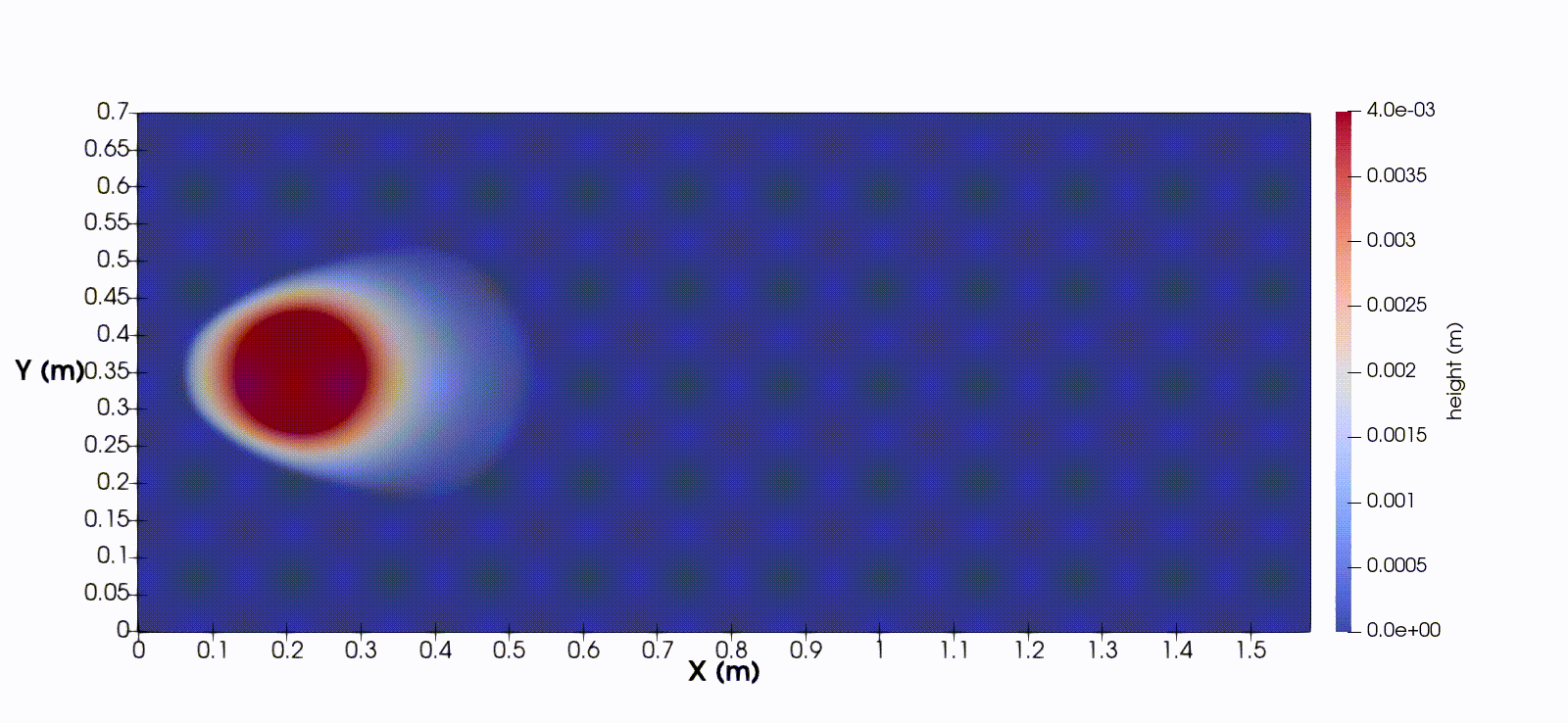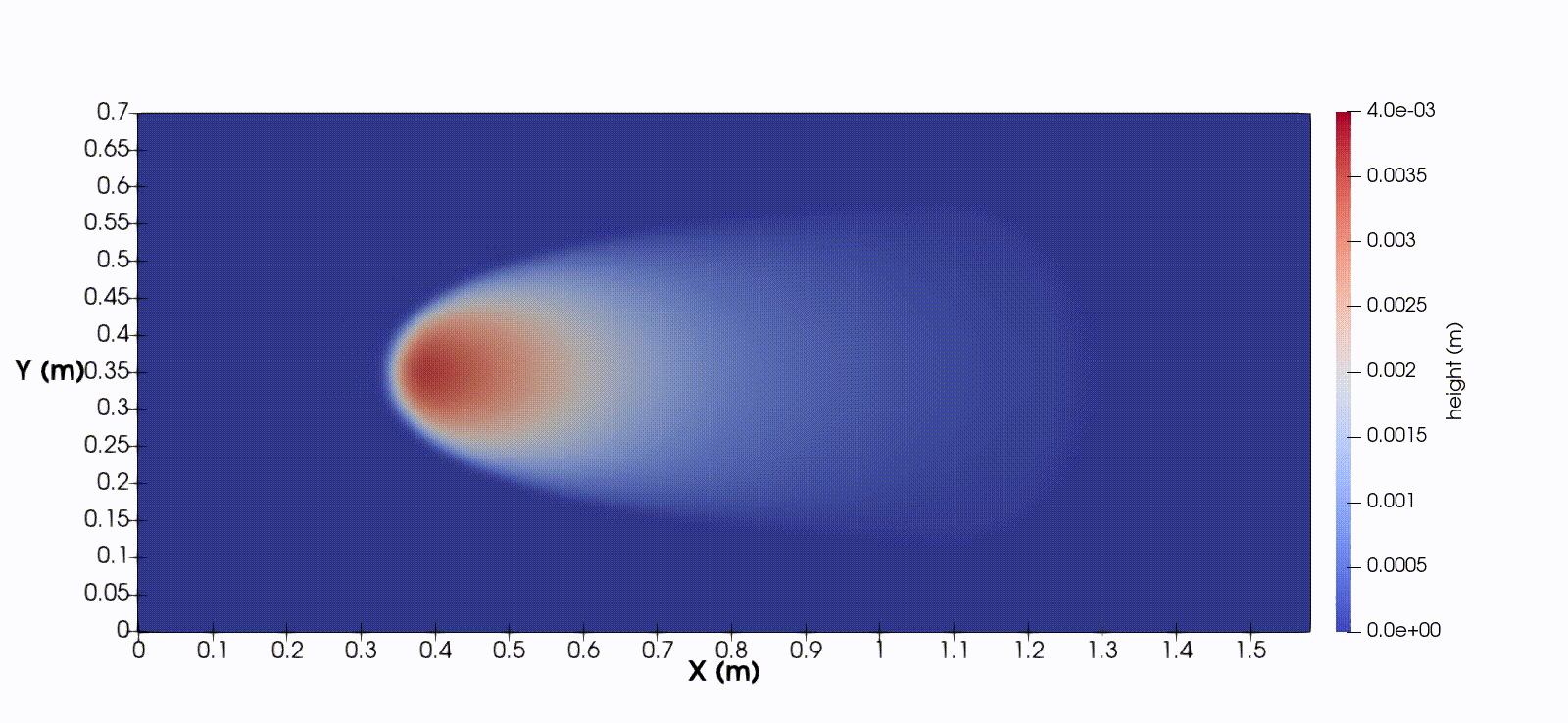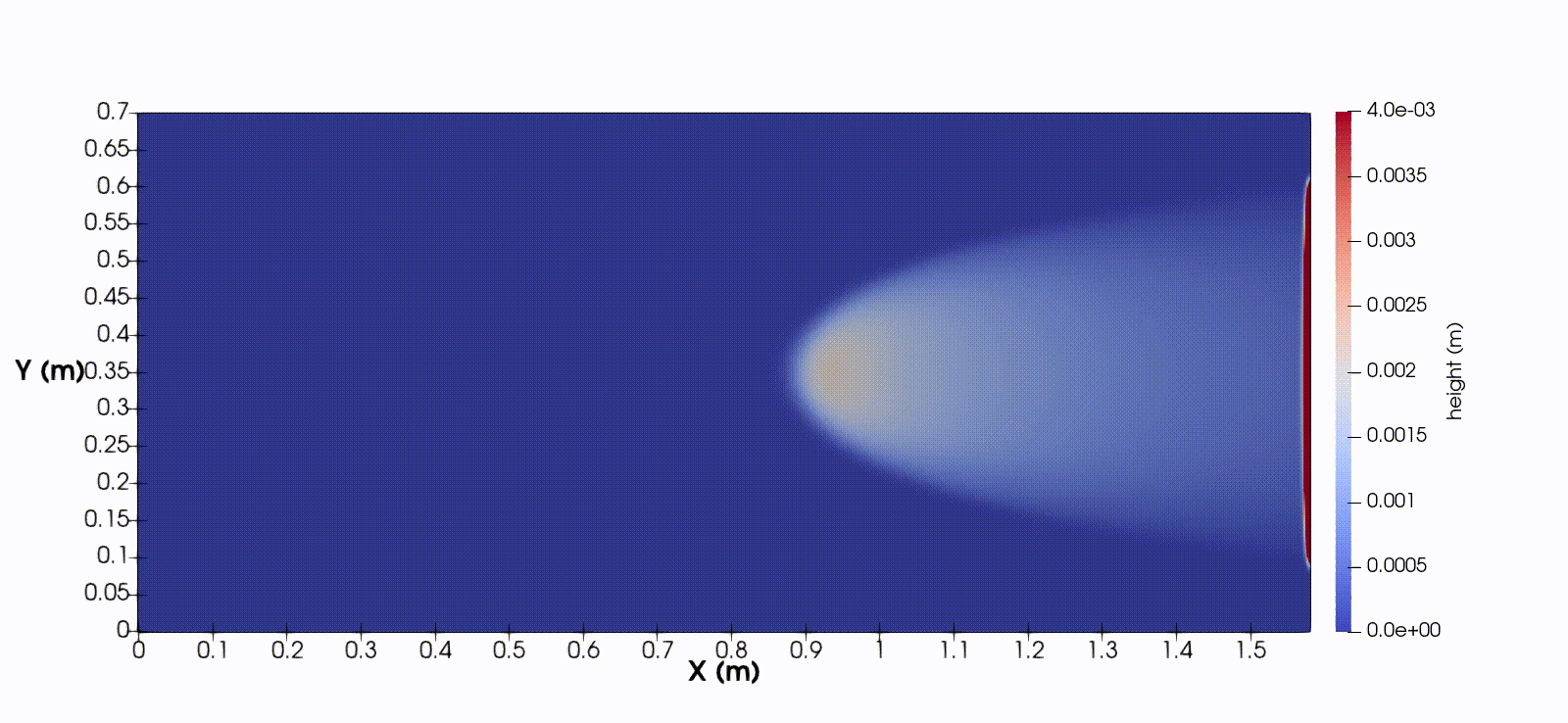
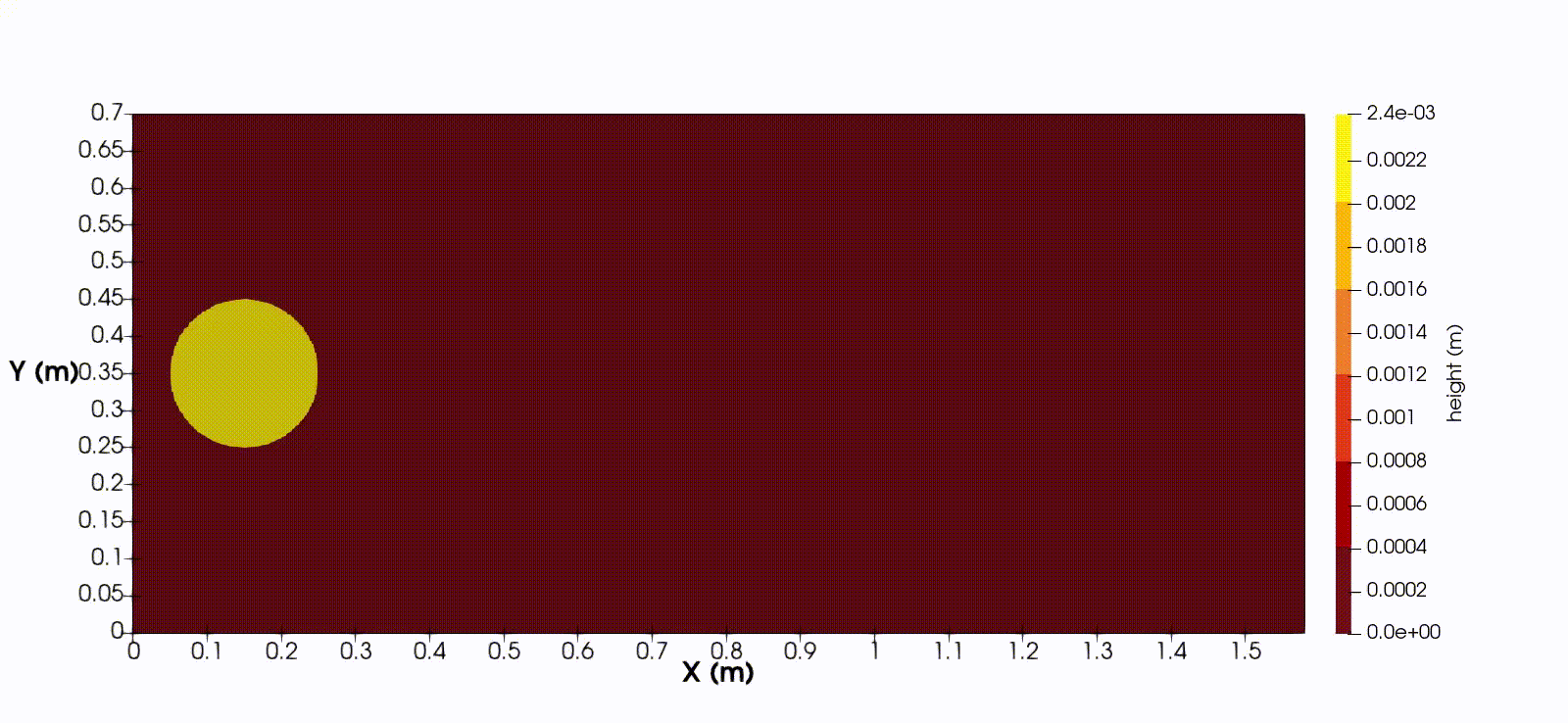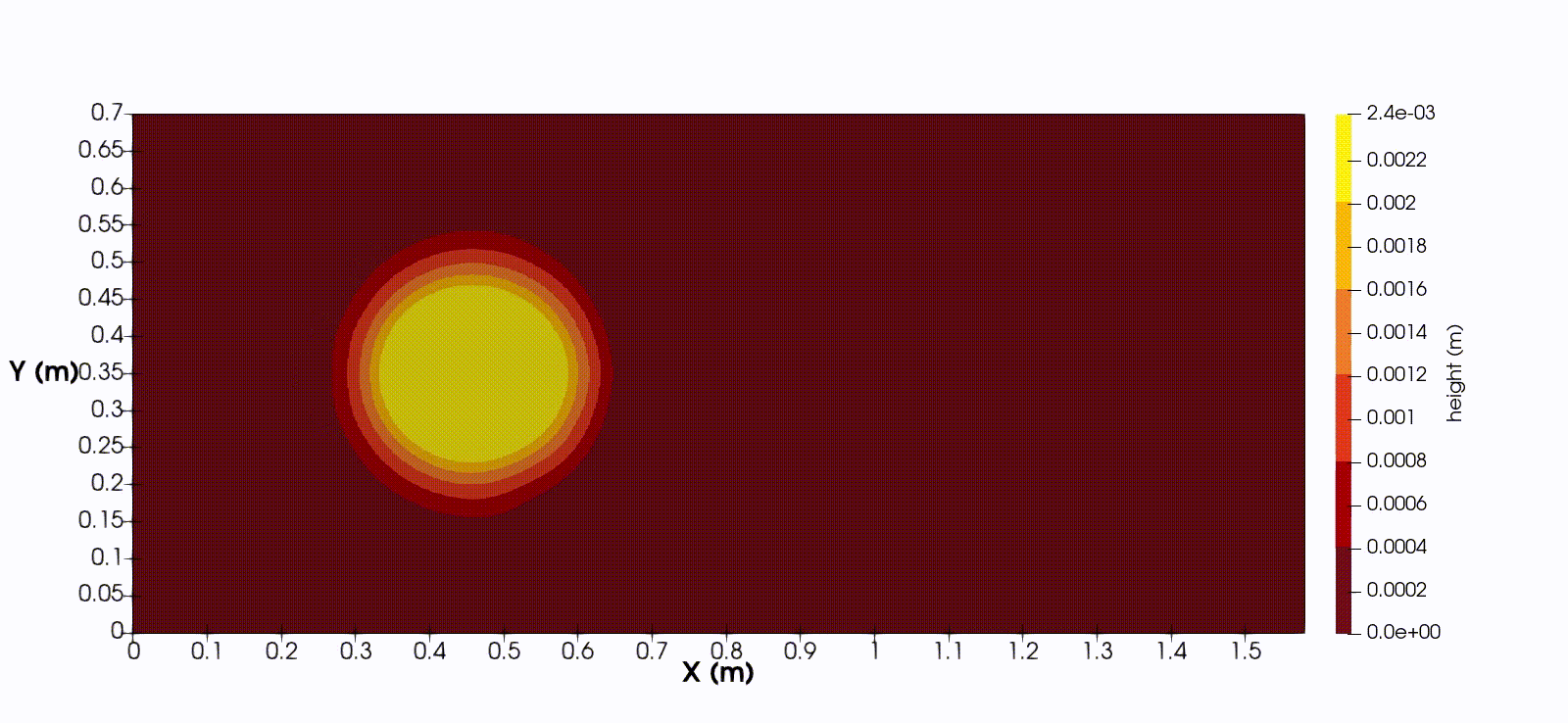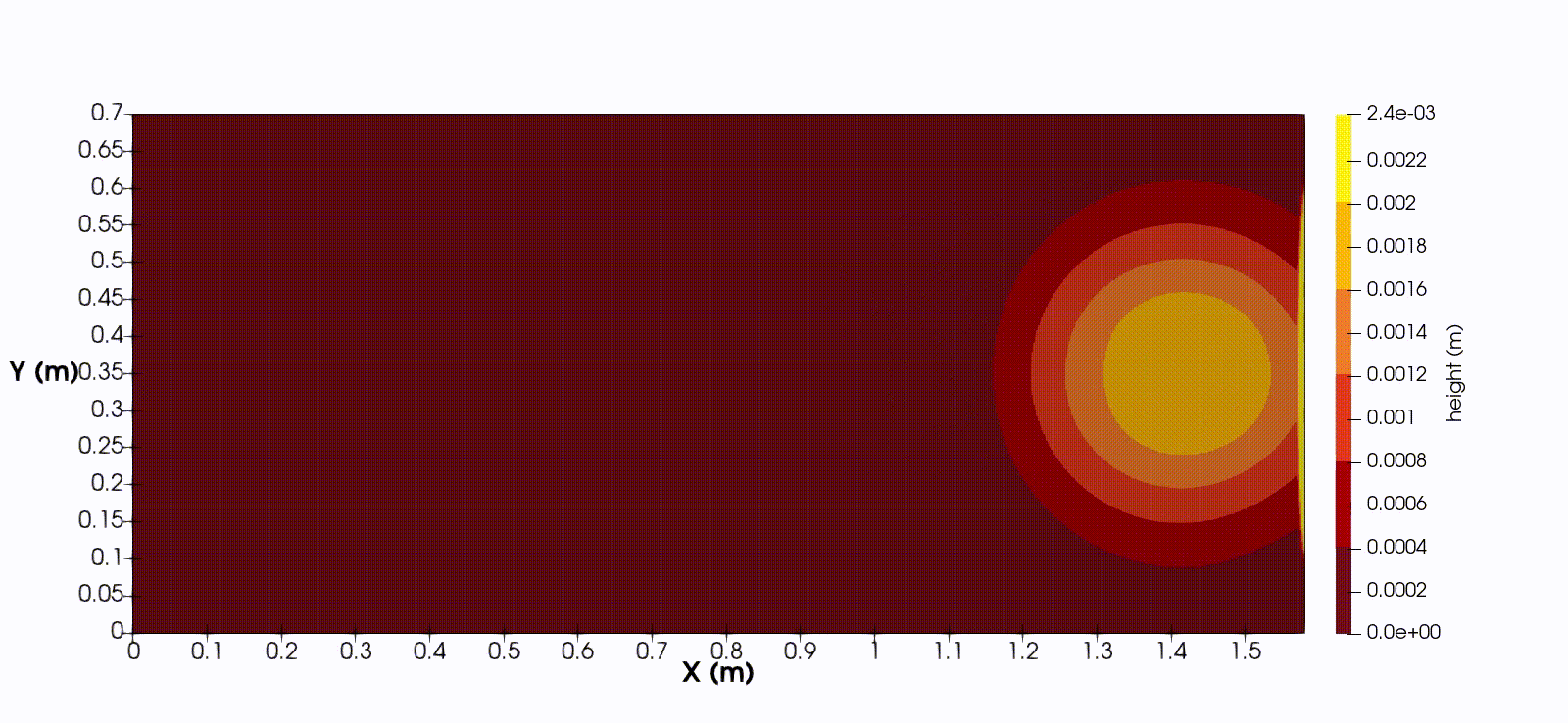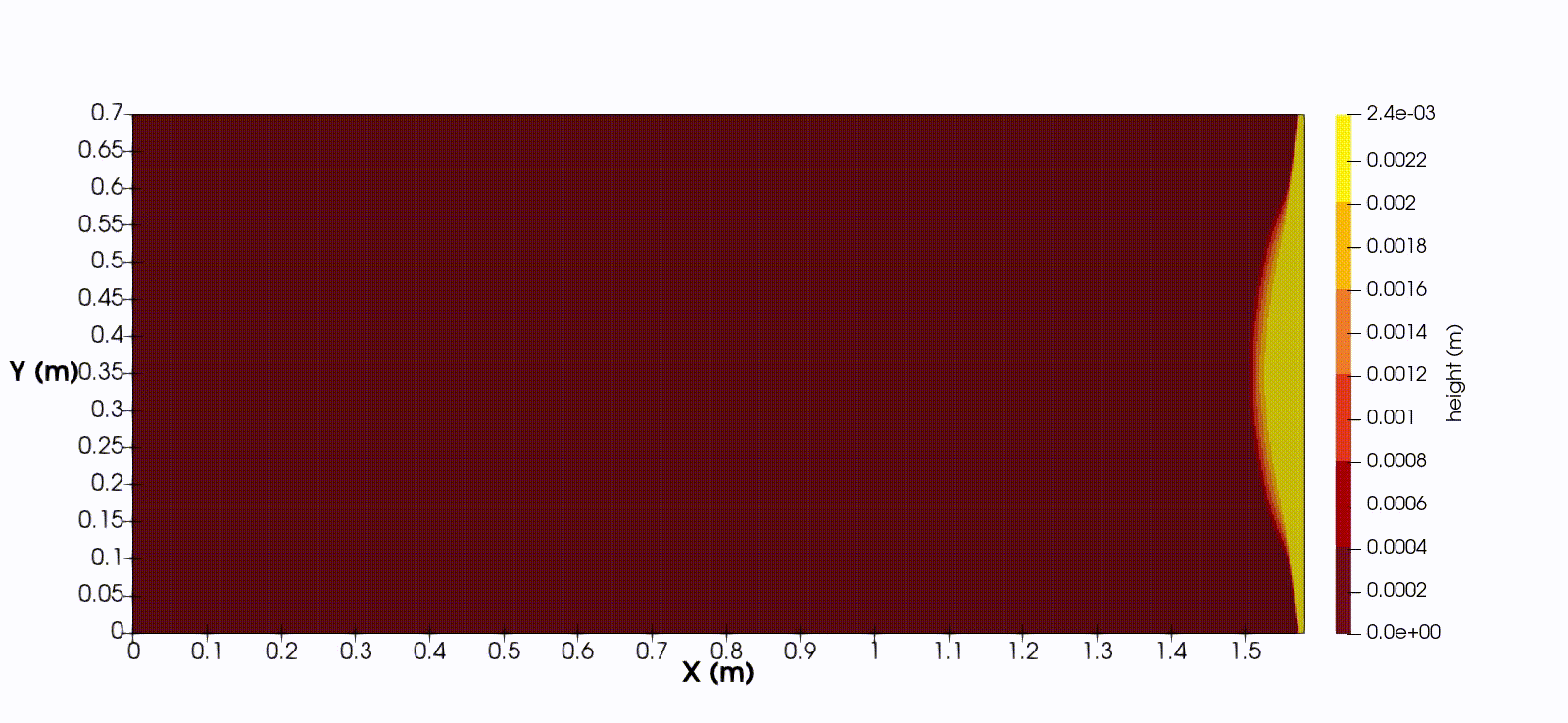
In one spatial dimension, the equations takes the form
$$ h_t + (hu)_x = 0, \quad (hu)_t + (hu^2 + \frac{1}{2}gh^2)_x = ghb_x - \frac{1}{\rho}(f_C + f_V), $$
where \( h, v \) is the depth and velocity of the flow and \( b \) is the topography and \( g \) is gravity. The friction forces are represented by the Coulomb friction \( f_C \) and the Voellmy friction \( f_V \) defined according to
$$ f_C = \mu \rho gh\cos(\theta)\frac{u}{|u|}, \quad f_V = \rho \frac{g}{\xi}|u|u, $$
where \( \theta \) is the slope angle of the topography, \( \mu = \tan(\phi) \), where \( \phi \) is the (basal) friction angle and \( \xi \) is the Voellmy friction parameter.
The full 2D equations including more complicated friction laws and material-dependent properties are given for an inclined plane by
\begin{eqnarray*}\frac{\partial}{\partial t} \begin{pmatrix} h\\hu\\hv \end{pmatrix} + \frac{\partial}{\partial x} \begin{pmatrix} hu\\hu^2 + \frac{1}{2} \cdot g\cos(\zeta)h^2\\huv \end{pmatrix} + \frac{\partial}{\partial y} \begin{pmatrix} hv\\huv\\hv^2 + \frac{1}{2} \cdot g\cos(\zeta)h^2 \end{pmatrix} +D(x) + D(y) = \begin{pmatrix} 0\\hg\sin(\zeta)-\mu\frac{u}{\sqrt{u^2+v^2}}hg\cos(\zeta)\\-\mu\frac{v}{\sqrt{u^2+v^2}}hg\cos(\zeta) \end{pmatrix}, \end{eqnarray*}
and
\begin{eqnarray*}D(x)=\begin{pmatrix} 0\\ -\nu\sqrt{h}(1.5\cdot\frac{\partial h}{\partial x}\frac{\partial u}{\partial x} + h\frac{\partial^2 u}{\partial x^2})\\ -0.5\cdot\nu\sqrt{h}(1.5\cdot\frac{\partial h}{\partial x}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})+h(\frac{\partial u}{\partial y \partial x}+\frac{\partial^2 v}{\partial x^2})) \end{pmatrix}, \end{eqnarray*}
\begin{eqnarray*}D(y)=\begin{pmatrix} 0\\ -0.5\cdot\nu\sqrt{h}(1.5\cdot\frac{\partial h}{\partial y}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})+h(\frac{\partial^2 u}{\partial y^2}+\frac{\partial v}{\partial x \partial y}))\\ -\nu\sqrt{h}(1.5\cdot\frac{\partial h}{\partial y}\frac{\partial v}{\partial y} + h\frac{\partial^2 v}{\partial y^2}) \end{pmatrix}, \end{eqnarray*}
where \( \zeta \) is the angle of inclination of the inclined plane.
The coefficient of basal friction \( \mu(Fr,h) \) is a piecewise function and the coefficient of viscosity \( \nu \) is a function of the material parameters. The complete expression for \( \mu(Fr,h) \) and \( \nu \) can be found in literature.
The ncp term requires the calculation of partial derivatives of \( h \), \( u \) and \( v \). These derivatives are calculated by finite difference schemes using a 9-point stencil (cf. fig below).

We use the notation: \( u(C2) \) = value of \( u \) in cell \( C2 \). The derivatives in cell 5 are calculated as follows:
\begin{eqnarray*}\frac{\partial u}{\partial x} &=& \frac{u(C5)-u(C4)}{\Delta x}\\ \frac{\partial u}{\partial y} &=& \frac{u(C5)-u(C8)}{\Delta y}\\ \frac{\partial^2 u}{\partial x^2} &=& \frac{u(C6)-2u(C5)+u(C4)}{(\Delta x)^{2}}\\ \frac{\partial^2 u}{\partial y^2} &=& \frac{u(C2)-2u(C5)+u(C8)}{(\Delta y)^{2}}\\ \frac{\partial^2 u}{\partial x \partial y} &=& \frac{u(C3)-u(C1)-u(C9)+u(C7)}{4\cdot \Delta x\cdot \Delta y}\\ \end{eqnarray*}
Similarly, derivatives of \( h \) and \( v \) are calculated.